Probability Integral Transform, A Proof
This post elucidates the connection between the generalized inverse, the cdf, the quantile function, and the uniform distribution.
Dustin Lennon
September 2018
https://dlennon.org/archive/20180914_prob
This work was originally published as an Inferentialist blog post.
Synopsis
Synopsis
The probability integral transform is a fundamental concept in statistics that connects the cumulative distribution function, the quantile function, and the uniform distribution. We motivate the need for a generalized inverse of the CDF and prove the result in this context.
Definitions
Definitions
Suppose \(U\) is the uniform distribution on \([0,1]\) , and \(F\) is the cumulative distribution of the random variable, \(Y\) , i.e.
\[ \begin{gather*} P\left( Y \leq y \right) = F(y) \end{gather*} \]
and define the inverse cdf — the quantile function — as
\[ F^{-1}(u) = \min \left\{ y : F(y) \geq u \right\} \]
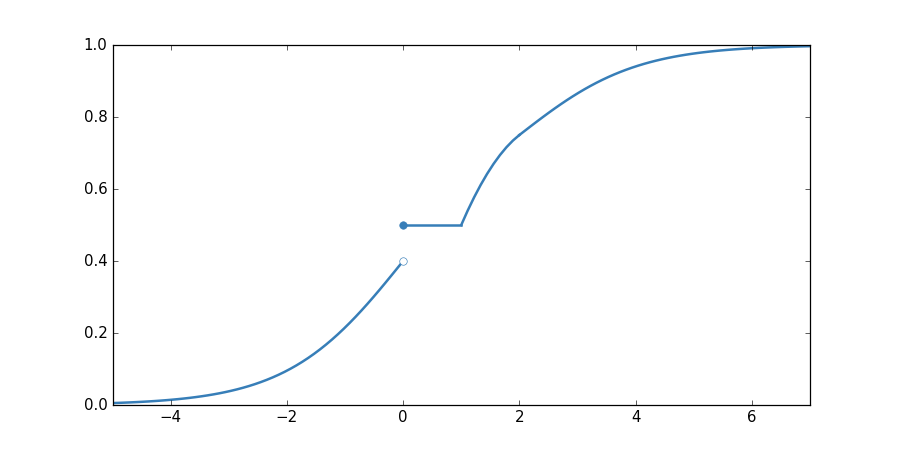
Recall that probability distributions — cdfs — are right continuous and monotonically increasing. However, as the example shows, they may also have flat sections and discontinuities. Indeed, the flat sections motivate the definition of the inverse cdf as a minimum. Thus, in the example, while \(F\) maps every point in the interval \([0,1]\) to \(0.5\), the preimage of the same interval is the single point, \(0\).
The Main Result
The Main Result
The key result is:
\[ P\left(F^{-1}(U) \leq y \right) = F(y) \]
That is, \(F^{-1}(U)\) and \(Y\) have the same distribution.
Proof
The proof isn’t particularly complicated, but it relies on two identities that follow from the definition of the inverse cdf.
First,
\[ u \leq F(F^{-1}(u)) \]
This follows from the definition as \(F^{-1}(u)\) is the smallest value of \(y\) for which \(F(y) \geq u\).
Second,
\[ F^{-1}(F(y)) \leq y \]
Using the definition, write the left hand side, with a change of index, as
\[ \begin{align*} F^{-1}(F(y)) & = \min \left\{ z : F(z) \geq F(y) \right \} \\ & \leq y \end{align*} \]
The inequality follows from the following argument. The flat section of the example shows that it is possible to have \(z\) less than \(y\). However, right-continuity implies that \(z\) may never exceed \(y\).
The main result is a statement about probabilities. As such, we can proceed by showing the following:
\[ F^{-1}(U(\omega)) \leq y \iff U(\omega) \leq F(y) \]
In what follows, let \(u = U(\omega)\).
The forward implication
We first show
\[ F^{-1}(u) \leq y \implies u \leq F(y) \]
Suppose \(F^{-1}(u) \leq y\).
Then, since \(F\) is monotonic, we can apply it to both sides of the inequality without issue:
\[ F(F^{-1}(u)) \leq F(y) \]
Combining this with the first of the above identities,
\[ u \leq F(F^{-1}(u)) \leq F(y) \]
Hence,
\[ F^{-1}(u) \leq y \implies u \leq F(y) \]
The reverse implication
The argument is similar. Note that \(F^{-1}\) is also monotonic. Thus, \(u \leq F(y)\) implies
\[ \begin{align*} F^{-1}(u) & \leq F^{-1}(F(y)) \\ & \leq y \end{align*} \]
and the result follows after applying the second of the above identities:
\[ u \leq F(y) \implies F^{-1}(u) \leq y \]
