Reproducing Results: ARM, Chapter 4
This notebook reproduces tables and figures in ARM, Chapter 4 [GH07]
Dustin Lennon
March 2021
https://dlennon.org/archive/20210303_armch04
ARM04: Linear regression: before and after fitting the model
ARM04: Linear regression: before and after fitting the model
Section 4.1: Linear transformations
Section 4.1: Linear transformations
# Standard imports
import numpy as np
import pandas as pd
import scipy.stats
import statsmodels.api as sm
import statsmodels.formula.api as smf
import patsy
import matplotlib.pyplot as plt
import matplotlib.ticker as mticker
# Custom imports
import common
import datasets
import arm
import summary
import pydlennon.extensions.matplotlib
from pydlennon.contexts.seeded_rng import SeededRng
# Set up the notebook session
from common import session
session._update(usetex=False, fontscale=1.0, seed=1111)
# Set up the summary factory
summarize = summary.Factory()
# Load the earnings dataset
dsf = datasets.Factory()
df = dsf('armch04a.earnings')
# Preview the table
df.head()
| earnings | height | male | |
|---|---|---|---|
| record_id | |||
| 3 | 50000.0 | 74.0 | 1 |
| 4 | 60000.0 | 66.0 | 0 |
| 5 | 30000.0 | 64.0 | 0 |
| 9 | 51000.0 | 63.0 | 0 |
| 10 | 9000.0 | 64.0 | 0 |
Equation 4.1
# Fit a linear model
y,X = patsy.dmatrices("earnings ~ height", data=df, return_type='dataframe')
model = sm.OLS(y,X).fit()
summarize(model)
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| Intercept | -6.052e+04 | 1.04e+04 | -5.809 | 0.000 | -8.1e+04 | -4.01e+04 |
| height | 1255.9797 | 155.063 | 8.100 | 0.000 | 951.713 | 1560.247 |
| Statistics | |
|---|---|
| n | 1059 |
| k | 2 |
| R-squared | 0.058 |
| residual sd | 19307.173 |
Figure 4.1
# Plot points
x = df.height
with SeededRng(100) as rng:
jx = x + rng.uniform(-0.2, 0.2, size=len(x))
# Set up figure, axes
fig = plt.figure(figsize=(10,4))
ax1 = fig.add_subplot(1,2,1)
ax2 = fig.add_subplot(1,2,2)
for ax in [ax1,ax2]:
ax.scatter(jx,y,s=3)
ax.abline(*model.params)
ax.set_xlabel('height')
ax.set_ylabel('earnings')
ax1.xaxis.set_major_locator( mticker.MultipleLocator(5) )
ax2.set_xlim((0,78))
ax2.set_ylim((-100000, 210000));
# OLS parametric bootstrap
with SeededRng(101) as rng:
beta_sim = arm.sim(model, 50, rng)
for beta in beta_sim:
intercept,slope = beta
ax1.abline(intercept, slope, color='gray', alpha=0.25, zorder=1)
ax2.abline(intercept, slope, color='gray', alpha=0.25, zorder=1)
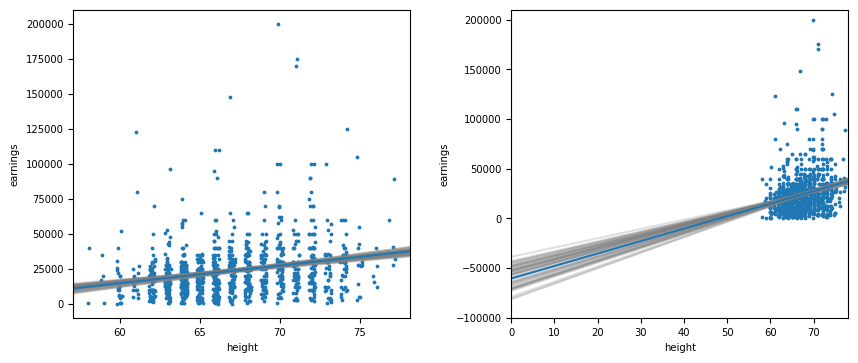
The figure on the right shows the difficulty associated with interpretation of the intercept estimate.
Section 4.2: Centering and standardizing, especially for models with interactions
Section 4.2: Centering and standardizing, especially for models with interactions
df = dsf("armch04.childiq", refresh=True)
df.head()
| kid_score | mom_hs | mom_iq | mom_age | mom_work | |
|---|---|---|---|---|---|
| 0 | 65 | 1 | 121.117529 | 27 | 4 |
| 1 | 98 | 1 | 89.361882 | 25 | 4 |
| 2 | 85 | 1 | 115.443165 | 27 | 4 |
| 3 | 83 | 1 | 99.449639 | 25 | 3 |
| 4 | 115 | 1 | 92.745710 | 27 | 4 |
y,X = patsy.dmatrices("kid_score ~ mom_hs + mom_iq + mom_hs:mom_iq", data=df, return_type='dataframe')
model = sm.OLS(y,X).fit()
summarize(model)
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| Intercept | -11.4820 | 13.758 | -0.835 | 0.404 | -38.523 | 15.559 |
| mom_hs | 51.2682 | 15.338 | 3.343 | 0.001 | 21.122 | 81.414 |
| mom_iq | 0.9689 | 0.148 | 6.531 | 0.000 | 0.677 | 1.260 |
| mom_hs:mom_iq | -0.4843 | 0.162 | -2.985 | 0.003 | -0.803 | -0.165 |
| Statistics | |
|---|---|
| n | 434 |
| k | 4 |
| R-squared | 0.230 |
| residual sd | 17.971 |
Centering by subtracting the mean of the data
With the interaction term, any interpretation of coefficients must be predicated on mom_iq being zero. This is a scenario which isn’t meaningful. Interpretation is far simpler after adjusting the variables.
# more interpretable; using stateful transforms
formula = "kid_score ~ center(mom_hs) + center(mom_iq) + center(mom_hs):center(mom_iq)"
y,X0 = patsy.dmatrices(formula, data=df)
model = sm.OLS(y,X0).fit()
summarize(model)
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| Intercept | 87.6389 | 0.908 | 96.565 | 0.000 | 85.855 | 89.423 |
| center(mom_hs) | 2.8408 | 2.427 | 1.171 | 0.242 | -1.929 | 7.610 |
| center(mom_iq) | 0.5884 | 0.061 | 9.712 | 0.000 | 0.469 | 0.707 |
| center(mom_hs):center(mom_iq) | -0.4843 | 0.162 | -2.985 | 0.003 | -0.803 | -0.165 |
| Statistics | |
|---|---|
| n | 434 |
| k | 4 |
| R-squared | 0.230 |
| residual sd | 17.971 |
formula = "kid_score ~ I(mom_hs-0.5) + I(mom_iq - 100) + I(mom_hs-0.5)*I(mom_iq-100)"
y,X1 = patsy.dmatrices(formula, data=df)
model = sm.OLS(y, X1, data=df).fit()
summarize(model)
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| Intercept | 86.8273 | 1.213 | 71.561 | 0.000 | 84.442 | 89.212 |
| I(mom_hs - 0.5) | 2.8408 | 2.427 | 1.171 | 0.242 | -1.929 | 7.610 |
| I(mom_iq - 100) | 0.7268 | 0.081 | 8.960 | 0.000 | 0.567 | 0.886 |
| I(mom_hs - 0.5):I(mom_iq - 100) | -0.4843 | 0.162 | -2.985 | 0.003 | -0.803 | -0.165 |
| Statistics | |
|---|---|
| n | 434 |
| k | 4 |
| R-squared | 0.230 |
| residual sd | 17.971 |
# perhaps even easier to interpret; in particular, compare to above
formula = "kid_score ~ mom_hs + center(mom_iq) + mom_hs:center(mom_iq)"
y,X1 = patsy.dmatrices(formula, data=df)
model = sm.OLS(y, X1, data=df).fit()
summarize(model)
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| Intercept | 85.4069 | 2.218 | 38.502 | 0.000 | 81.047 | 89.767 |
| mom_hs | 2.8408 | 2.427 | 1.171 | 0.242 | -1.929 | 7.610 |
| center(mom_iq) | 0.9689 | 0.148 | 6.531 | 0.000 | 0.677 | 1.260 |
| mom_hs:center(mom_iq) | -0.4843 | 0.162 | -2.985 | 0.003 | -0.803 | -0.165 |
| Statistics | |
|---|---|
| n | 434 |
| k | 4 |
| R-squared | 0.230 |
| residual sd | 17.971 |
type(df)
pandas.core.frame.DataFrame
Stateful Transforms (patsy)
The patsy package uses stateful transforms to maintain a separation between training and test data. This is encapsulated by the build_design_matrices function. Using the statsmodel formula interface simplifies the transformation process.
# Using the statsmodels formula interface
model_smf = smf.ols(formula, data=df).fit()
all(model_smf.params == model.params)
True
# Transform some data
z = df.iloc[0:5]
xz = patsy.build_design_matrices([X1.design_info], z)[0]
# Predictions
np.c_[
model.predict(xz, transform=False),
model_smf.predict(z)
]
array([[98.48151832, 98.48151832],
[83.09226994, 83.09226994],
[95.73163912, 95.73163912],
[87.98094406, 87.98094406],
[84.73212235, 84.73212235]])
Standardizing by subtracting the mean and dividing by 2 standard deviations
ARM recommends a standardization that divides by two standard deviations. Implementing this in patsy looks like the following:
class ArmStandardize(patsy.state.Standardize):
def transform(self, x, center=True, rescale=True, ddof=0):
x = patsy.state.asarray_or_pandas(x, copy=True, dtype=float)
x_2d = patsy.state.atleast_2d_column_default(x, preserve_pandas=True)
if center:
x_2d -= self.current_mean
if rescale:
x_2d /= 2*np.sqrt(self.current_M2 / (self.current_n - ddof))
return patsy.state.pandas_friendly_reshape(x_2d, x.shape)
arm_standardize = patsy.stateful_transform(ArmStandardize)
formula = "kid_score ~ arm_standardize(mom_hs) + arm_standardize(mom_iq) + arm_standardize(mom_hs):arm_standardize(mom_iq)"
model = smf.ols(formula, data=df).fit()
summarize(model)
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| Intercept | 87.6389 | 0.908 | 96.565 | 0.000 | 85.855 | 89.423 |
| arm_standardize(mom_hs) | 2.3313 | 1.991 | 1.171 | 0.242 | -1.583 | 6.245 |
| arm_standardize(mom_iq) | 17.6313 | 1.815 | 9.712 | 0.000 | 14.063 | 21.199 |
| arm_standardize(mom_hs):arm_standardize(mom_iq) | -11.9089 | 3.989 | -2.985 | 0.003 | -19.749 | -4.068 |
| Statistics | |
|---|---|
| n | 434 |
| k | 4 |
| R-squared | 0.230 |
| residual sd | 17.971 |
Interpretability of the above model is now on a roughly common scale. Because we divide by two standard deviations, the standardized mom_hs takes on values near -0.5 and 0.5, and the coefficient reflects a comparison of a (nearly) unit change in mom_hs. That is, we recover an estimate that captures the full range of mom_hs.
4.3 Correlation and “regression to the mean”
4.3 Correlation and “regression to the mean”
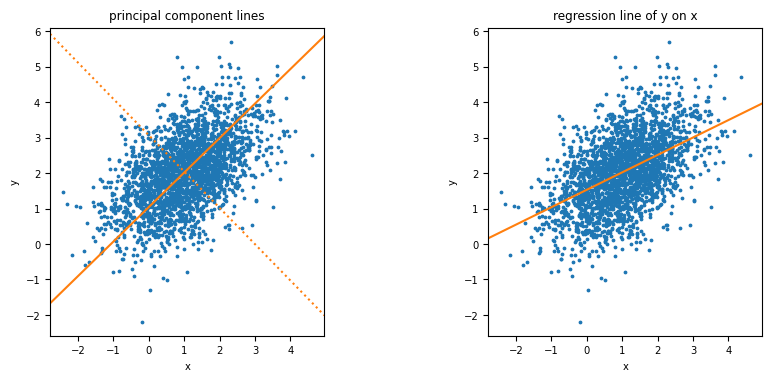
Figure 4.2
# Simulate correlated MVN data
mu = np.array([2,1], dtype=float)
Omega = np.array([[1, 0.5], [0.5, 1]])
with SeededRng(102) as rng:
xy = rng.multivariate_normal(mu, Omega, size=2500)
xydf = pd.DataFrame(xy, columns=['y', 'x'])
X = xydf.values
# regresion line
model = smf.ols("y ~ x", data=xydf).fit()
intercept,slope = model.params
# principal component lines
mu = np.mean(X, axis=0)
w,V = np.linalg.eig( np.cov(X.T) )
pc_slopes = -V[1,:] / V[0,:]
pc_intercepts = mu[0] - mu[1:] * pc_slopes
x = xydf.x
y = xydf.y
# Set up the figure
fig = plt.figure(figsize=(10,4))
ax1 = fig.add_subplot(1,2,1)
ax2 = fig.add_subplot(1,2,2)
for ax in [ax1,ax2]:
ax.scatter(x,y,s=3)
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_aspect(1)
ax1.set_title('principal component lines')
ax1.abline(pc_intercepts[0], pc_slopes[0], color=common.colors[1])
ax1.abline(pc_intercepts[1], pc_slopes[1], color=common.colors[1], ls=":")
ax2.set_title('regression line of y on x')
ax2.abline(intercept, slope, color=common.colors[1]);
Section 4.4: Logarithmic transformation
Section 4.4: Logarithmic transformation
Height and earnings example
df = dsf('armch04b.earnings')
formula = "np.log(earnings) ~ height"
y,X = patsy.dmatrices(formula, data=df, return_type="dataframe")
model = sm.OLS(y,X).fit()
summarize(model)
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| Intercept | 5.7785 | 0.451 | 12.815 | 0.000 | 4.894 | 6.663 |
| height | 0.0588 | 0.007 | 8.743 | 0.000 | 0.046 | 0.072 |
| Statistics | |
|---|---|
| n | 1192 |
| k | 2 |
| R-squared | 0.060 |
| residual sd | 0.893 |
Figure 4.3
Figure 4.3
x = X.height
with SeededRng(103) as rng:
jx = x + rng.uniform(-0.2,0.2,size=len(x))
# helper function to plot a transformed curve
def xplt(ax, beta, **kw):
xlim = ax.get_xlim()
x = np.linspace(*ax.get_xlim(), num=100)
y = np.exp(beta[0] + x * beta[1])
ax.plot(x,y, **kw)
ax.set_xlim(xlim)
# Set up the figure
fig = plt.figure(figsize=(10,4))
ax1 = fig.add_subplot(1,2,1)
ax2 = fig.add_subplot(1,2,2)
for ax in [ax1,ax2]:
ax.set_xlabel('height')
ax1.scatter(jx,y,s=3)
ax1.abline(*model.params)
ax1.set_ylabel("log(earnings)")
ax1.set_title("Log regression on log scale")
ax2.scatter(jx,np.exp(y),s=3)
xplt(ax2, model.params)
ax2.set_ylabel("earnings")
ax2.set_title("Log regression plotted on original scale")
# OLS parametric bootstrap
with SeededRng(104) as rng:
beta_sim = arm.sim(model, 50, rng)
for beta in beta_sim:
intercept,slope = beta
ax1.abline(intercept, slope, color='gray', alpha=0.25, zorder=1)
xplt(ax2, beta, color='gray', alpha=0.25, zorder=1)
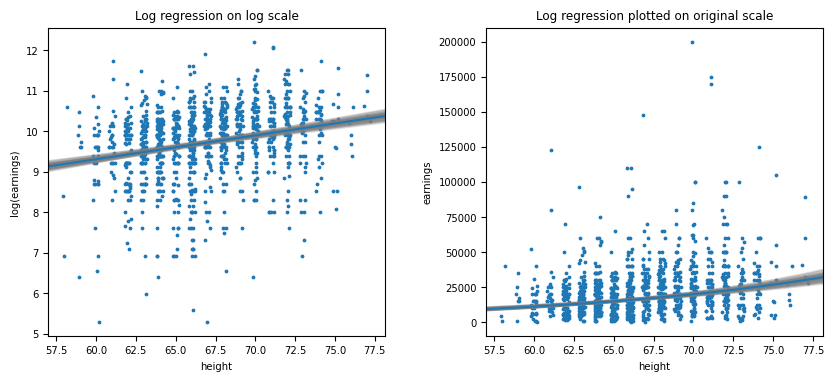
Figure 4.4
Figure 4.4
Omitted, expository.
Building a regression model on the log scale
formula = "np.log(earnings) ~ height + male"
model = smf.ols(formula, data=df).fit()
summarize(model)
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| Intercept | 8.1527 | 0.603 | 13.530 | 0.000 | 6.970 | 9.335 |
| height | 0.0207 | 0.009 | 2.218 | 0.027 | 0.002 | 0.039 |
| male | 0.4232 | 0.072 | 5.841 | 0.000 | 0.281 | 0.565 |
| Statistics | |
|---|---|
| n | 1192 |
| k | 3 |
| R-squared | 0.087 |
| residual sd | 0.881 |
Linear transformation to make coefficients more interpretable
formula = "np.log(earnings) ~ standardize(height) + male + standardize(height):male"
model = smf.ols(formula, data=df).fit()
summarize(model)
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| Intercept | 9.5266 | 0.045 | 210.878 | 0.000 | 9.438 | 9.615 |
| standardize(height) | 0.0654 | 0.050 | 1.304 | 0.193 | -0.033 | 0.164 |
| male | 0.4197 | 0.073 | 5.748 | 0.000 | 0.276 | 0.563 |
| standardize(height):male | 0.0286 | 0.072 | 0.400 | 0.690 | -0.112 | 0.169 |
| Statistics | |
|---|---|
| n | 1192 |
| k | 4 |
| R-squared | 0.087 |
| residual sd | 0.881 |
Section 4.5: Other transformations
Section 4.5: Other transformations
Figure 4.5
Omitted, unknown data source.
# A model using an ordered categorical variable, mother's work history after childbirth
df = dsf('armch04.childiq')
df['mom_work'] = df.mom_work.values.codes # this used to work w/o accessors...?
model = smf.ols("kid_score ~ C(mom_work)", data=df).fit()
summarize(model)
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| Intercept | 82.0000 | 2.305 | 35.568 | 0.000 | 77.469 | 86.531 |
| C(mom_work)[T.1] | 3.8542 | 3.095 | 1.245 | 0.214 | -2.229 | 9.937 |
| C(mom_work)[T.2] | 11.5000 | 3.553 | 3.237 | 0.001 | 4.517 | 18.483 |
| C(mom_work)[T.3] | 5.2098 | 2.704 | 1.927 | 0.055 | -0.105 | 10.524 |
| Statistics | |
|---|---|
| n | 434 |
| k | 4 |
| R-squared | 0.024 |
| residual sd | 20.230 |
Section 4.6: Building regression models for prediction
Section 4.6: Building regression models for prediction
Example: predicting the yields of mesquite bushes
df = dsf('armch04.mesquite', refresh=True)
df.head()
| group | diam_1 | diam_2 | total_height | canopy_height | density | weight | |
|---|---|---|---|---|---|---|---|
| record_id | |||||||
| 1 | MCD | 1.8 | 1.15 | 1.30 | 1.00 | 1 | 401.3 |
| 2 | MCD | 1.7 | 1.35 | 1.35 | 1.33 | 1 | 513.7 |
| 3 | MCD | 2.8 | 2.55 | 2.16 | 0.60 | 1 | 1179.2 |
| 4 | MCD | 1.3 | 0.85 | 1.80 | 1.20 | 1 | 308.0 |
| 5 | MCD | 3.3 | 1.90 | 1.55 | 1.05 | 1 | 855.2 |
# Initial model
formula = "weight ~ diam_1 + diam_2 + canopy_height + total_height + density + group"
model = smf.ols(formula, data=df).fit()
summarize(model)
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| Intercept | -728.5929 | 147.159 | -4.951 | 0.000 | -1026.250 | -430.935 |
| group[T.ALS] | -363.2951 | 100.184 | -3.626 | 0.001 | -565.936 | -160.654 |
| diam_1 | 189.6690 | 112.760 | 1.682 | 0.101 | -38.410 | 417.748 |
| diam_2 | 371.4621 | 124.378 | 2.987 | 0.005 | 119.883 | 623.041 |
| canopy_height | 355.6653 | 209.843 | 1.695 | 0.098 | -68.782 | 780.113 |
| total_height | -101.7325 | 185.574 | -0.548 | 0.587 | -477.091 | 273.626 |
| density | 131.2542 | 34.355 | 3.820 | 0.000 | 61.764 | 200.744 |
| Statistics | |
|---|---|
| n | 46 |
| k | 7 |
| R-squared | 0.848 |
| residual sd | 268.960 |
# Descriptive statistics
s = df.describe().T
s['IQR'] = s.loc[:,"75%"] - s.loc[:,"25%"]
s.loc[:,['min','25%','50%','75%','max', 'IQR']]
| min | 25% | 50% | 75% | max | IQR | |
|---|---|---|---|---|---|---|
| diam_1 | 0.80 | 1.4000 | 1.950 | 2.475 | 5.2 | 1.0750 |
| diam_2 | 0.40 | 1.0000 | 1.525 | 1.900 | 4.0 | 0.9000 |
| total_height | 0.65 | 1.2000 | 1.500 | 1.700 | 3.0 | 0.5000 |
| canopy_height | 0.50 | 0.8625 | 1.100 | 1.300 | 2.5 | 0.4375 |
| density | 1.00 | 1.0000 | 1.000 | 2.000 | 9.0 | 1.0000 |
| weight | 60.20 | 219.6250 | 361.850 | 688.725 | 4052.0 | 469.1000 |
# Multiplicative model
formula = "np.log(weight) ~ np.log(diam_1) + " \
"np.log(diam_2) + np.log(canopy_height) + " \
"np.log(total_height) + np.log(density) + group"
model = smf.ols(formula, data=df).fit()
summarize(model)
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| Intercept | 5.3515 | 0.170 | 31.391 | 0.000 | 5.007 | 5.696 |
| group[T.ALS] | -0.5834 | 0.129 | -4.534 | 0.000 | -0.844 | -0.323 |
| np.log(diam_1) | 0.3938 | 0.282 | 1.397 | 0.170 | -0.177 | 0.964 |
| np.log(diam_2) | 1.1512 | 0.210 | 5.477 | 0.000 | 0.726 | 1.576 |
| np.log(canopy_height) | 0.3732 | 0.281 | 1.330 | 0.191 | -0.194 | 0.941 |
| np.log(total_height) | 0.3943 | 0.313 | 1.260 | 0.215 | -0.239 | 1.027 |
| np.log(density) | 0.1093 | 0.122 | 0.896 | 0.376 | -0.137 | 0.356 |
| Statistics | |
|---|---|
| n | 46 |
| k | 7 |
| R-squared | 0.887 |
| residual sd | 0.329 |
# Minimalist model
df['canopy_volume'] = df.diam_1 * df.diam_2 * df.canopy_height
formula = "np.log(weight) ~ np.log(canopy_volume)"
model = smf.ols(formula, data=df).fit()
summarize(model)
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| Intercept | 5.1697 | 0.083 | 62.066 | 0.000 | 5.002 | 5.338 |
| np.log(canopy_volume) | 0.7224 | 0.055 | 13.234 | 0.000 | 0.612 | 0.832 |
| Statistics | |
|---|---|
| n | 46 |
| k | 2 |
| R-squared | 0.799 |
| residual sd | 0.414 |
# Adding semantic, interpretable predictors
df['canopy_area'] = df.diam_1 * df.diam_2
df['canopy_shape'] = df.diam_1 / df.diam_2
formula = "np.log(weight) ~ np.log(canopy_volume) + np.log(canopy_area) +" \
"np.log(canopy_shape) + np.log(total_height) + np.log(density) + group"
model = smf.ols(formula, data=df).fit()
summarize(model)
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| Intercept | 5.3515 | 0.170 | 31.391 | 0.000 | 5.007 | 5.696 |
| group[T.ALS] | -0.5834 | 0.129 | -4.534 | 0.000 | -0.844 | -0.323 |
| np.log(canopy_volume) | 0.3732 | 0.281 | 1.330 | 0.191 | -0.194 | 0.941 |
| np.log(canopy_area) | 0.3993 | 0.294 | 1.357 | 0.183 | -0.196 | 0.994 |
| np.log(canopy_shape) | -0.3787 | 0.231 | -1.642 | 0.109 | -0.845 | 0.088 |
| np.log(total_height) | 0.3943 | 0.313 | 1.260 | 0.215 | -0.239 | 1.027 |
| np.log(density) | 0.1093 | 0.122 | 0.896 | 0.376 | -0.137 | 0.356 |
| Statistics | |
|---|---|
| n | 46 |
| k | 7 |
| R-squared | 0.887 |
| residual sd | 0.329 |
# Reduced model, post fit assessment
formula = "np.log(weight) ~ np.log(canopy_volume) + np.log(canopy_area) + group"
model = smf.ols(formula, data=df).fit()
summarize(model)
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| Intercept | 5.2244 | 0.088 | 59.197 | 0.000 | 5.046 | 5.403 |
| group[T.ALS] | -0.5269 | 0.116 | -4.558 | 0.000 | -0.760 | -0.294 |
| np.log(canopy_volume) | 0.6148 | 0.191 | 3.215 | 0.003 | 0.229 | 1.001 |
| np.log(canopy_area) | 0.2889 | 0.238 | 1.215 | 0.231 | -0.191 | 0.768 |
| Statistics | |
|---|---|
| n | 46 |
| k | 4 |
| R-squared | 0.873 |
| residual sd | 0.337 |
Bibliography
Bibliography
[GH07] Gelman, A., and Hill, J. (2007). Data Analysis Using Regression and Multilevel/Hierarchical Models. Chapter 3.
