

To call in the statistician after the experiment is done may be no more than asking him to perform a post-mortem examination: he may be able to say what the experiment died of.
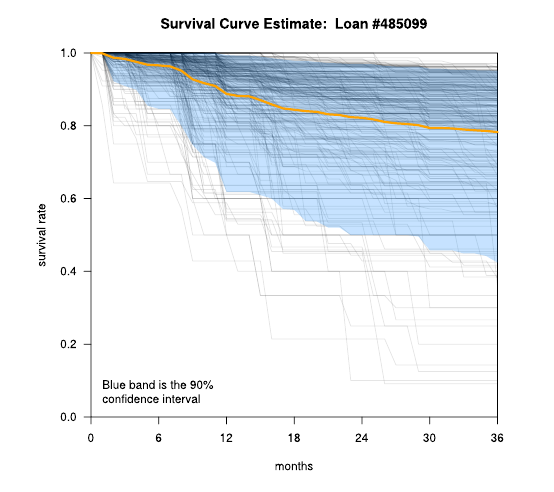
The paper describes a strategy for constructing optimal portfolios of peer-to-peer loans. We develop a novel, non-parametric surivival model designed to statistically characterize each loan, and we use this characterization to estimate the net present value and volatility of the underlying cash flow.
The optimal portfolio strategy has an annual return of above 12%. This constitutes a 30% to 50% improvement over a strategy based only on pre-assigned loan grades.
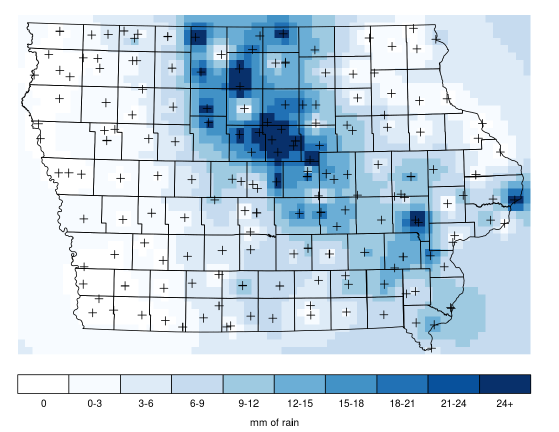
The paper considers the problem of estimating Iowa soybean yield from historical, daily precipitation data.
We introduce a hierarchical, averaging operator that, for each county, aggregates temporal precipitation data over dyadic, nested intervals. The domain of the averaging operator can be interpreted as the kernel of an integral transform, a function to be estimated from the data. We use a Lasso regression to compute this estimate, taking advantage of the sparsity induced by the Lasso on the dyadically nested domain.
In this case, a simplest model might estimate the per-county yield by the average, taken per-county and over several years. Using the sparse functional model strategy described here, we show a dramatic improvement over that simple model showing a reduction in the residual sum of squares for a test set of holdout counties, by 66%.
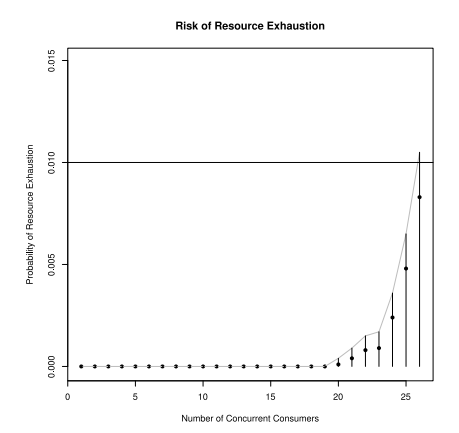
We investigate, in the context of a simple example, a statistical method for quantifying the risk associated with resource allocation in the case of oversubscription. We formulate the problem in a mathematical context and establish business level parameters which govern the rate of resource exhaustion and the confidence we can assert in controlling that rate.
To validate the procedure, we run a simulation over different resource consumption scenarios. In the non-oversubscribed case, we have a 26.4% usage rate; 73.6% of our resource pool goes unused.
Using the strategy described in the paper, we can guarantee, with 95% confidence, that resources will be available 99% of the time. This relaxation provides a 2.5x increase in utilization, and the median usage rate jumps to 66.7%.
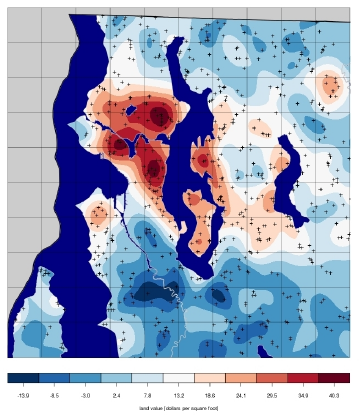
This "job-talk" presentation describes a Bayesian, hedonic pricing model used to estimate sales prices of single family homes in the Seattle area. As a consequence of the underlying model, we also obtain confidence intervals on our estimates.
The development proceeds as follows:
The Inferentialist logo leverages some classical ideas from computational geometry. Take a look at what's behind the scenes when we blend math and aesthetics.
Things you always wanted to know about but were afraid to ask:
